PROGRAMASI LINIER (LINIER PROGRAMING = LP)

Programasi Linier adalah suatu cara untuk menyelesaikan persoalan pengalokasian sumber daya yang terbatas diantara beberapa aktivitas yang bersaing dengan cara terbaik yang mungkin dilakukan. Misalnya : persoalan pengalokasian fasilitas  produksi, penjadwalan produksi, pemilihan pola pengiriman dan sebagainya.

Programasi Linier menggunakan model matematis untuk menyelesaikan persoalan-persoalan yang dihadapi. Sifat linier di sini mengandung arti bahwa seluruh fungsi matematis dalam model yang digunakan merupakan fungsi linier, sedangkan kata programa merupakan sinonim untuk perencanaan. Dengan demikian programa linier adalah perencanaan aktivitas-aktivitas untuk memperoleh suatu hasil yang optimum, yaitu suatu hasil yang mencapai tujuan terbaik diantara seluruh alternatif yang laik (feasible).

Menggunakan bahasa matematis, programa linier adalah suatu model optimasi persamaan linier berkenaan dengan pembatas-pembatas (kendala-kendala) linier yang dihadapi. Masalah programa linier berarti masalah pencarian nilai-nilai optimum (maksimum atau minimum) suatu fungsi linier pada suatu sistem atau sekumpulan pembatas atau pembatas linier. Fungsi linier yang hendak dicari nilai optimumnya berbentuk sebuah persamaan linier atau pertidaksamaan linier dan disebut fungsi pembatas atau fungsi kendala

Rumusan model persoalan programa linier memiliki beberapa karakteristik sebagai berikut:

a.     Variabel Keputusan

Variabel keputusan adalah variabel yang menguraikan secara lengkap keputusan-keputusan yang akan dibuat. Variabel keputusan ini biasanya disimbolkan dengan X_j dimana  j = 1,2,3,....,n.

b.     Fungsi Tujuan

Fungsi tujuan ( Z ) merupakan fungsi dari variabel keputusan yang akan dimaksimumkan (misalnya: pendapatan, keuntungan) atau diminimumkan (misalnya: ongkos, biaya). Rumusan fungsi tujuan sebagai berikut: Z=C₁X₁+C₂X₂+C₃X₃+.........C_nX_n

c.      Pembatas/Kendala

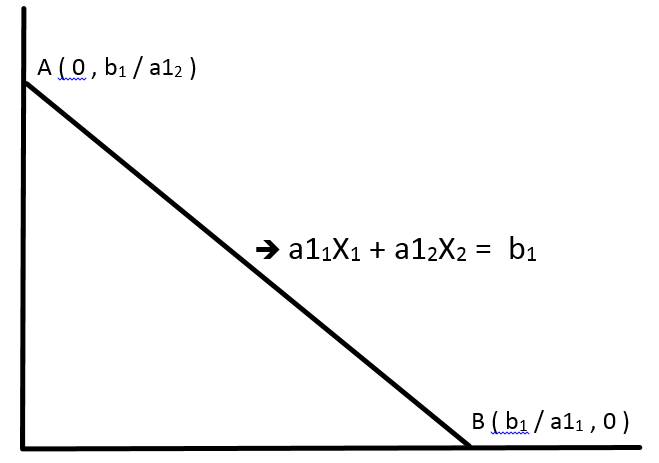
Pembatas merupakan kendala yang dihadapi sehingga kita tidak dapat menentukan nilai-nilai variabel keputusan secara sembarangan. Pembatas-pembatas dinyatakan dengan menggunakan variabel-variabel keputusan yang relevan. Rumusan fungsi pembatas/kendala sebagai berikut:

a1₁X₁+ a1₂X₂+ a1₃X₃+...... a1_nX_n {≤b₁ atau; ≥b₁ atau; =b₁} _{<=hasil persamaan/pertidaksamaan}

a2₁X₁+ a2₂X₂+ a2₃X₃+...... a1_nX_n {≤b₂ atau; ≥b₂ atau; =b₂} _{<=hasil persamaan/pertidaksamaan}  

am_nX_n+ am_nX_n+ am_nX_n+...... am_nX_n {≤b_m atau; ≥b_m atau; =b_m} _{<=hasil persamaan/pertidaksamaan}

Koefisien dari variabel keputusan pada fungsi pembatas (yaitu: a1₁, a1₂, ....., am_n) disebut koefisien teknologi, sedangkan bilangan yang ada pada sisi kanan setiap fungsi pembatas (yaitu: b₁, b₂, b₃,......, b_m) disebut ruas kanan pembatas.

d.     Pembatas Tanda

Pembatas tanda adalah pembatas yang menjelaskan apakah variabel keputusan diasumsikan hanya berharga nun-negatif(≥ 0) atau boleh positif(> 0) atau boleh negatif(< 0). Dalam kasus-kasus ekonomi, pembatas tanda biasanya berharga nun-negatif(≥ 0).

Masalah Programa Linier tak lain adalah masalah optimasi bersyarat yakni pencarian nilai maksimum (maksimasi) atau minimum (minimasi) suatu fungsi tujuan berkenaan dengan pembatas-pembatas yang harus dipenuhi.

Masalah maksimasi dan minimasi dalam model programa linier secara umum dirumuskan sebagai berikut:

a.     Masalah Maksimasi

Maksimumkan fungsi tujuan

Z=C₁X₁+C₂X₂+C₃X₃+.........C_nX_n

Terhadap pembatas:

a1₁X₁ + a1₂X₂ + a1₃X₃ +.......... a1_nX_n  ≤ b₁

a2₁X₁ + a2₂X₂ + a2₃X₃+......... .a1_nX_n  ≤ b₂  

am_nX_n + am_nX_n + am_nX_n +...... am_nX_n  ≤ b_m

dimana X_j ≥ 0      j = 1,2,3,.....,n

b.     Masalah Minimasi

Z=C₁X₁+C₂X₂+C₃X₃+.........C_nX_n

Terhadap pembatas:

a1₁X₁ + a1₂X₂ + a1₃X₃ +.......... a1_nX_n  ≥ b₁

a2₁X₁ + a2₂X₂ + a2₃X₃+......... .a1_nX_n  ≥ b₂

am_nX_n + am_nX_n + am_nX_n +...... am_nX_n  ≥ b_m

dimana X_j ≥ 0      j = 1,2,3,.....,n

Catatan:

fungsi-fungs pembatas dalam masalah maksimasi tidak senantiasa berbentuk (≤) seperti nampak pada bentuk umum diatas, melainkan ada juga yang berbentuk (≥) atau (=) Begitu pula dalam masalah minimasi, fungsi-fungsi pembatasnya tidak senantiasa (≥) melainkan ada juga yang berbentuk (≤) atau (=)


lanjutan materinya dapat dilihat disini